LZ
Table of Contents
Let's make a hilbert curve on is page in Clojure (the one ❤) and allow the reader to manipulate the code in-place.
what is a hilbert curve?
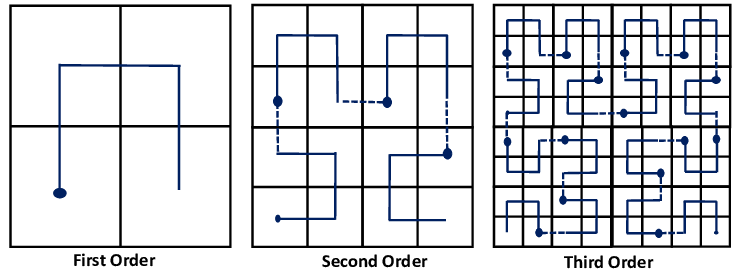
A Hibert Curve is a space-filling fractal. it's useful for mapping 2 dimensional space stuff onto 1 dimension. I like it because it looks good.
what is scittle?
Scittle is is a small Clojure interpreter designed to be embedded inside web pages using html <script> tags. For example to evaluate code input by the user.
Aside
It's great how simple Scittle is to use inside this blog. I'm writing in an org file in Emacs. I embed some script tags in a export block. Like so:
#+begin_export html <script src="https://cdn.jsdelivr.net/npm/scittle@0.5.14/dist/scittle.js" type="application/javascript"></script> <script type="application/x-scittle"> (defn my-alert [] (js/alert "You clicked!")) ;; export function to use from JavaScript: (set! (.-my_alert js/window) my-alert) </script> <body> <button onclick="my_alert()"> Click me! </button> </body> #+end_export
Then I run my regular build script and away we go, running Clojure in my blog post via skittle via js via org-mode-export with practically no extra configuration at all. That's wild.
handle user input code
First let's make a textarea in html to get the user input. We'd like a button to click evaluate what the user enters. Then output the result beneath.
<script type="application/x-scittle"> (defn set-output-area [v output-id] (-> (js/document.getElementById output-id) (.-innerHTML) (set! v))) (defn try-eval [v] (try (js/scittle.core.eval_string v) (catch js/Error e (str "ERROR: " e)))) (defn read-eval-input [input-id] (-> input-id js/document.getElementById .-value try-eval)) (set! (.-read_input js/window) #(set-output-area (read-eval-input "code-area") "output-area")) </script> <body> <textarea id="code-area" class="code-textarea"> (take 21 ((fn fib [a b] (lazy-seq (cons a (fib b (+ a b))))) 0 1)) </textarea> <button onclick="read_input()">eval</button> <p id="output-area">...</p> </body>
...
Right nice.
drawing
I think the easiest way to do this will be with canvas.
<canvas id="first-canvas" width="400" height="400" class="canvas"></canvas> <script type="application/x-scittle"> (def c (js/document.getElementById "first-canvas")) (def ctx (.getContext c "2d")) (.moveTo ctx 50 50) (.lineTo ctx 50 150) (.lineTo ctx 150 150) (.lineTo ctx 150 50) (.stroke ctx) </script>
Let's have it so that the user can pass in an vector of points that the line will go through:
<canvas id="points-canvas" width="200" height="200" class="canvas"></canvas> <script type="application/x-scittle"> (def c (js/document.getElementById "user-points-canvas")) (def ctx (.getContext c "2d")) (defn try-eval [v] (try (js/scittle.core.eval_string v) (catch js/Error e (str "ERROR: " e)))) (defn read-eval-input [input-id] (-> input-id js/document.getElementById .-value try-eval)) (defn draw-line-from-points [context points] (.clearRect context 0 0 (.-width c) (.-height c)) (.beginPath context) (.moveTo context (-> points first first) (-> points first second)) (doseq [[x y] (rest points)] (.lineTo context x y)) (.stroke context)) (set! (.-read_points js/window) #(->> (read-eval-input "points-input") (draw-line-from-points ctx))) </script> <body> <textarea id="points-input" class="code-textarea"> [[50 50] [50 150] [150 150] [150 50]] </textarea> <button onclick="read_points()">Draw points</button> </body>
Now it's just a matter of choosing the right points.
making the hilbert curve
How this fractal works is that there are four patterns, and each one of these four pattern can be split up into quarters, and each one of those quarters can be swapped for one of the original four patterns. Recursion.
Here's the details of that mapping:
(def rules {:A {:path [[0 0] [0 1] [1 1] [1 0]] :next-iteration [:D :A :A :B]} :B {:path [[1 1] [0 1] [0 0] [1 0]] :next-iteration [:C :B :B :A]} :C {:path [[1 1] [1 0] [0 0] [0 1]] :next-iteration [:B :C :C :D]} :D {:path [[0 0] [1 0] [1 1] [0 1]] :next-iteration [:A :D :D :C]}})
So each path has four points we can think about it as tracing three sides of a square in a specific order. Let's say the origin is top-left, then the path for :A is from the origin, across the top, down the right side and from right to left across the bottom. The sides and the order we go through the points is all significant.
Let's think about our canvas as a square split up into square cells. The number of cells is controlled by the number of iterations we perform (4n). Each cell contains a pattern, we need to have the right order of cells and the right pattern for each. So we'll aim for a sequence of cells, where a cell is an [x, y] vector identifying the cell, and a pattern. Here's the zero'th iteration with a single cell in it:
(def init [{:cell [0 0] :pattern :A}])
To turn this into the next iteration we need to subdivide the space into four cells, and then add a pattern for each one:
(defn ->subcells [{:keys [cell pattern]}] (let [top-left-subcell (map (partial * 2) cell) path-step->subcells (fn [path-step] (map + top-left-subcell path-step)) path (->> rules pattern :path (map path-step->subcells)) cell-patterns (-> rules pattern :next-iteration)] (map (fn [cell pattern] {:cell cell :pattern pattern}) path cell-patterns))) (map ->subcells init) ;=> (({:cell (0 0), :pattern :D} ; {:cell (0 1), :pattern :A} ; {:cell (1 1), :pattern :A} ; {:cell (1 0), :pattern :B}))
Okay, now we would like to iterate that, each time concatenating the results into a single sequence.
(defn hilbert-curve-cells [iterations] (-> (iterate #(->> % (map ->subcells) (apply concat)) init) (nth iterations))) (hilbert-curve-cells 2) ;=> ({:cell (0 0), :pattern :A} ; {:cell (1 0), :pattern :D} ; {:cell (1 1), :pattern :D} ; {:cell (0 1), :pattern :C} ; {:cell (0 2), :pattern :D} ; {:cell (0 3), :pattern :A} ; {:cell (1 3), :pattern :A} ; {:cell (1 2), :pattern :B} ; {:cell (2 2), :pattern :D} ; {:cell (2 3), :pattern :A} ; {:cell (3 3), :pattern :A} ; {:cell (3 2), :pattern :B} ; {:cell (3 1), :pattern :C} ; {:cell (2 1), :pattern :B} ; {:cell (2 0), :pattern :B} ; {:cell (3 0), :pattern :A})
Lovely. Okay we don't care about the patterns any more once we have finished iterating, but we do want to change from cells to points on the canvas. Let's grab the ordered cells and use the canvas dimensions to turn them into points.
(defn cells->points [cells iterations canvas-width] (let [width-in-cells (js/Math.pow 2 iterations) step-width (/ canvas-width width-in-cells)] (->> cells (map :cell) (map #(map * 1% 2%) (repeat [step-width step-width]))))) (defn hilbert-curve-points [iterations canvas-width] (-> (hilbert-curve-cells iterations) (cells->points iterations canvas-width))) (hilbert-curve-points 2 400) ;=> ((0.0 0.0) ; (100.0 0.0) ; (100.0 100.0) ; (0.0 100.0) ; (0.0 200.0) ; (0.0 300.0) ; (100.0 300.0) ; (100.0 200.0) ; (200.0 200.0) ; (200.0 300.0) ; (300.0 300.0) ; (300.0 200.0) ; (300.0 100.0) ; (200.0 100.0) ; (200.0 0.0) ; (300.0 0.0))
That's it. Muck about with the code and see what results you can get.